Na jednom z predmetových cvičení na univerzite som dostal za úlohu vypracovať zadanie na tému primitívneho Turingového stroja. Nikdy predtím so o Turingovom stroji nepočul a vôbec som nevedel ako mám postupovať. Zadanie nevyžadovalo znalosť programovania, preto jeho vypracovanie nie je vo forme kódu ale vo forme písaných inštrukcii.
Zadanie príkladu:
Popíšte konštrukciu kontrolného kódu, ktorý akceptuje reťazec tvaru:
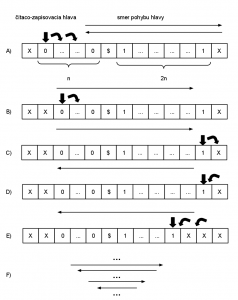
X 0…(nx0)…0$1……(2nx1)……1 X (obrázok časť A) pre n>1 pomocou inštrukcii l if sig then (sig’, o, l).
{Inštrukciu môžeme prečítať ako: Ak sme na mieste inštrukcie l, ak prehliadané políčko obsahuje sig, potom prepíšeme sig na sig’, posunieme sa o o políčko ( do ľava = -1, stoj na pozícii = 00 , do prava = +1 ) a vykonáme (nasledujúcu) inštrukciu l. Vysvetlenie: X – hraničný znak, $ – deliaci znak, 0 – nula, 1 – jednotka}
Popis riešenia:
Jedná sa o primitívny Turingov stroj. Čítacia hlava sa pohybuje z ľava do prava a naspäť (obrázok časť A). Začíname na mieste prvej 0 z ľava a postupujeme podľa inštrukcii (hore). Pohybujeme sa do prava (obrázok časť B), až dôjdeme na X (obrázok časť C) a pohybujeme sa naspäť (obrázok časť D). To opakujeme toľkokrát, koľko je treba (obrázok časť F). Výsledkom kontrolného kódu bude buď vyhovujúci počet n na obidvoch stranách (nx0=2nx1) alebo nevyhovujúci stav (nevyhovujúce prípady).
Možné koncové prípady:
Začiatok:
X 0…0$1……1 X – Na jednej, aj druhej strane je určitý počet 0 a 1tiek.
Koniec – vyhovujúce vyhodnotenie:
X X…X$X……X X – Na oboch stranách bol rovnaký počet jednotiek a núl.
Koniec – nevyhovujúce vyhodnotenie:
a) X X…X0$X……X X
– Na ľavej strane bolo o jednu nulu viac ako jednotiek na pravej.
b) X X…X…00$X……X X
– Na ľavej srane bolo o niekoľko núl viac ako jednotiek na pravej.
c) X X…X$1X……X X
– Na pravej strane bolo o jednu jedntku viac ako na ľavej núl.
d) X X…X$11..X……X X
– Na pravej strane bolo o niekoľko jednotiek viac ako na ľavej strane núl.
Riešenie
Upozornenie : Je dôležité uvedomiť si, čo robia inštrukcie (italics v zadaní príkladu).
01. if 0 than (X,+1,02.) -- Prepíšeme 0 na X (hraničný znak) 02. if 0 than (0,+1,02.) -- Cyklus až kým sa nedôjde po $ 03. if $ than ($,+1,04.) 04. if 1 than (1,+1,04.) -- Cyklus až kým sa nedôjde po X 05. if X than (X,-1,06.) 06. if 1 than (X,-1,07.) -- Prepíšeme 1 na X (hraničný znak) 07. if 1 than (X,-1,08.) -- Prepíšeme 1 na X (hraničný znak) 08. if 1 than (1,-1,08.) -- Cyklus až kým sa nedôjde po $ 09. if $ than ($,-1,10.) 10. if 0 than (0,-1,10.) -- Cyklus až kým sa nedôjde po X 11. if X than (X,+1,12.) ======================== -- Koniec jednej otočky. 12. if 0 than (0,00,17.) ======================== -- Poistka. Kedže inštrukcie sa spracúvajú v smere zhora nadol, ak by tu nebol 12. bod, došlo by k tomu, že čítacia hlava sa posunie za znak $ a tam buď vyhodnotí stav alebo sa zasekne. To by potom odporovalo inštrukcii 17., ktorá je ešte pred $ znakom. Preto inštrukcia 12. je taká poistka, že pred $ nie je 0. Ak pred $ nie je nula, dostávame sa do jedného z možných koncových vyhodnotení. 13. if $ than ($,+1,14.) 14. if X than (X,00,23.) ======================== -- Vyhovujuce vyhodnotenie X X...X$X......X X, výsledok vyhovuje (nx0=2nx1) 15. if $ than ($,+1,16.) 16. if 1 than (1,00,22.) ======================== -- Nevyhovujúce vyhodnotenie c) X X...X$1X......X X a d) X X...X$11..X......X X. Na pravej strane je o niekoľko 1 viac ako na ľavej n 0liek. (<em>Na rozdiel od nevyhovujúceho vyhodnotenia a) a b) keď narazíme už na prvú 1tku vieme, že nevyhovuje. Pri a) b) môže byť najskôr viac 0iek a robí sa cyklus. Len tak informatívne ...</em>) 17. if 0 than (X,+1,18.) 18. if 0 than (0,+1,18.) -- Cyklus až kým sa nedôjde po $ 19. if $ than ($,+1,20.) 20. if X than (X,00,22.) ======================== -- Nevyhovujúce vyhodnotenie a) X X...X0$X......X X a b) X X...X...00$X......X X. Na ľavej strane je o niekoľko 0 viac ako na pravej xn 1tiek. 21. if 1 than (1,00,04.) ======================== -- Sme za $ znakom a môžeme pokračujeme odznova... 22. RETURN 23. ACCEPT
Update 18. 12. 2010
– Zmenil som obrázok, pridal som časť F) a následne dosadil do textu.
– Číslo 21. malo tvar “21. if 1 than (X,+1,04.)” a teda, po deliacom znaku $ menilo prvú 1 na X. To je samozrejme zle. Teraz ma tvar “if 1 than (1,00,04.)”. Tento tvar vyjadruje, že keď za $ znakom ide 1, možeme to chápať už ako časť nového cyklu a pokračovať od bodu 04.
Update 01. 05. 2011
Dozvedel som sa, že Alan Turing bol najväčší odborník na Počítačovú vedu v ľudskej histórii. Podieľal sa napr. na dešifrovaní a rozlúštení kódu Enigmi. Tento algoritmus som vytvoril bez znalosti pozadia Alana Turinga a Turingovho stroja (len na základe základných inštrukcii). Z letmého pohľadu na anglickú wikipédiu o Turingovom stroji sa môj algoritmus zdá správny. Odporúčam však radšej porovnať ho s obsahom wikipédie lepšie.
Update 05. 12. 2015
Pre pochopenie významu Alana Turinga pre súčastnú históriu odporúčam pozrieť si film v anglickom názve – The Imitation Game.
Kľúčové slová
Alan Turing, inštrukcie turingovho stroja, primitívny turingov stroj, Turing machine, Turingov stroj, Turing, kódovanie, algoritmus, kryptografia, matematika, computer science, počítačová veda

06. if 1 than (X,-1,07.)
— Prepíšeme 0 na X (hraničný znak)
07. if 1 than (X,-1,08.)
— Prepíšeme 0 na X (hraničný znak)
Nema byt: prepiseme 1 na X ?
Áno, máš pravdu. Opravené 🙂